14- Wind Load
Wind loads are mostly among the most critical design considerations for single-story steel buildings. These loads are thoroughly addressed in relevant structural design standards and manuals, which provide comprehensive procedures and criteria for their determination and application.
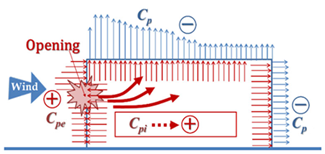
Design wind pressures for the main wind force resisting system of the enclosed and partially enclosed rigid and flexible buildings shall be determined by the following equation:
p=qGCp-qi(GCpi)
where:
Cp is external pressure coefficient
GCpi is internal pressure coefficient
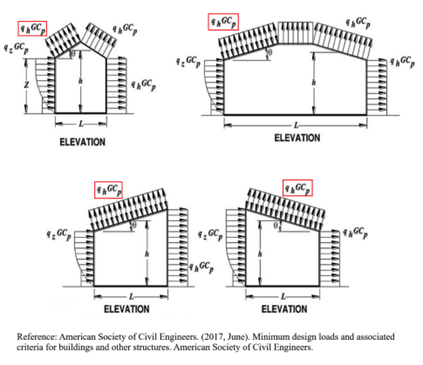
The external wind pressure acting on building roof can be directed either downward or upward.
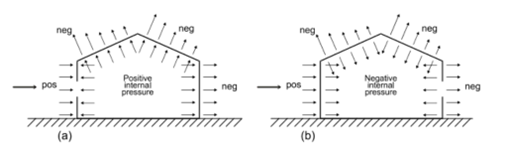
The internal wind pressure can also act either upward or downward on building surfaces.
Standards and manuals define the coefficient for internal and external pressures. Below the Tables from Minimum design loads and associated criteria for buildings and other structures, ASCE 07-16 is presented:
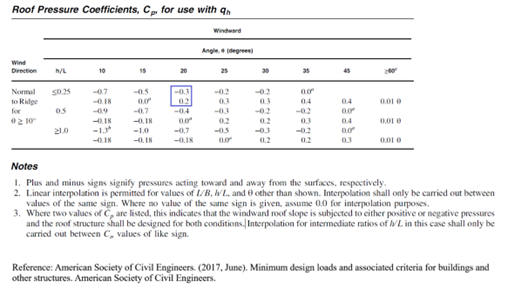

As shown above, for a certain sample these are two cases for external pressure, positive pressure and negative pressure (-0.3 & 0.2), and two cases for internal pressure, positive value and negative value (-0.18 & +0.18).
Therefore, four different cases exist in total.
(case a) P= qGCp (Upward)-qi(GCpi) (Positive)
(case b) P= qGCp (Upward)-qi(GCpi) (Negative)
(case c) P= qGCp (Downward)-qi(GCpi) (Positive)
(case d) P= qGCp (Downward)-qi(GCpi) (Negative)
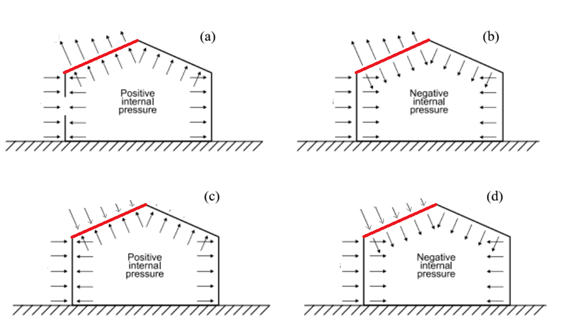
However, among these four cases, two cases represent the most critical conditions (Cases (a) and (d)).
When applying Case (d), downward external wind pressure combined with negative internal pressure, the resulting load is more severe in downward direction than that from Cases (a), (b), or (c).
Similarly, applying Case (a), upward external wind pressure combined with positive internal pressure, the resulting load is more severe in upward direction than that from Cases (b), (c), or (d).
Therefore, MkaPEB takes into account the two most critical cases.
This approach is not limited to ASCE 07-16 and ASCE 07-22 alone; similar methods for calculating wind loads are also referenced in other design standards. Therefore, the same approach is adopted for wind load calculations.
As an example, for a roof pitch angle of 5.7°, the values are calculated in accordance with EN 1991-1-4: Eurocode 1 – Actions on Structures, Part 1-4: General Actions – Wind Actions.
The pressure coefficient for Zone F is calculated by linear interpolation between the negative values −1.7- and −0.9, resulting in −1.644. Similarly, the corresponding value for the positive case is obtained as 0.014.
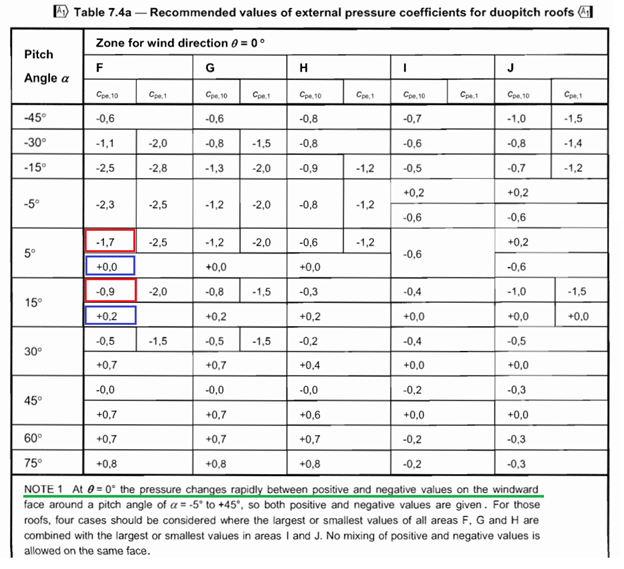
Reference: https://www.phd.eng.br/wp-content/uploads/2015/12/en.1991.1.4.2005.pdf, (Page: 47/149)
Moreover, for internal pressure both negative and positive values exist. For this example, according to EN 1991-1-4 chapter 7.2.9 note (2), -0.3 and +0.2.
Therefore, the most severe upward case (-1.644, and +0.2) , and the most severe downward case (+0.014, -0.3) are being considered.

Regarding the load combinations below, considering both cases is essential, because: the combination of dead load and wind (in the most severe upward case) may result in a large net upward force, and the combination of dead load, snow load, and wind (in the most severe downward case) may result in a large net downward force.
lc1) 1.4 D
lc2) 1.2 D + 0.3 S
lc3) 1.2 D + 1.0 S + 0.5 W
lc4) 1.2 D + 1.0 W + 0.3 S
lc5) 0.9D + 1.0 W
Ignoring either Case (a) or Case (d) may lead to critical design errors.
However, this oversight is occasionally made by some engineers. In an example presented in regulation on design, calculation, and construction principles of steel structures - application guide by T.C. ministry of environment and urbanization, this issue exists.
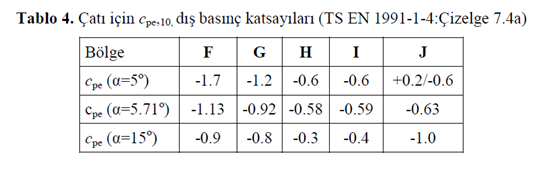
Firstly, It should be noted that in this table there is an error in interpolation and instead of -1.644, a value equal to -1.13 is presented.
Secondly, as can be seen, just the negative values for external pressure, case (a) and (b), are taken into account in this application guide.
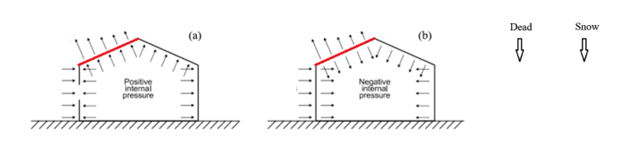
In this cases ((a) and (b)), increasing wind severity consistently reduces the net effect of dead and snow loads due to uplift. However, in cases where the wind acts downward (case (d)), a more severe wind load increases the total applied load by adding to the dead and snow loads.
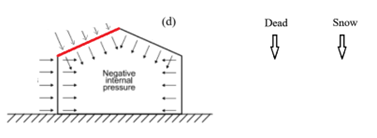
When designing structures, ignoring case (d)—downward external pressure combined with negative internal pressure—can lead to an unsafe design in many situations.